The interplay of group and topological structures

One of the permeating themes in mathematics is the study of structures. When we study a mathematical object, we hope to find out something nice about it. The more structures it possesses, the nicer it mathematically is, and the more relationships to other mathematical objects it can spawn.

In this article we would like to discuss two important structures in mathematics--group structure and topological structure--and how they interact. For the definitions of groups and topological spaces, see here and here.

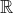
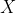
There are abundant examples of topological spaces which at the same time are group themselves. For instance, is a group with respect to addition, and a topological space, with open sets generated by open intervals. We say that the group structure is compatible with the topological structure of if left multiplication, right multiplication by any element, and taking inverse are continuous maps on . 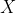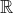So addition in is compatible with its standard topology. This definition is crucial in our discussion for the following two reasons. First, it ties the two structures together. Second, it excludes examples of topological spaces with pathological group structures which would be uninteresting. 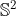Consider with its group multiplication defined by

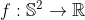
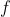
where is any set-theoretic bijection. We know that can be extremely sporadic.

Now here comes the question: given a topological space, does there always exist a compatible group structure?

Let's get our hands dirty by working out some concrete examples. We want to see if there is any compatible group structure in . If you are reading this article carefully enough, you may notice that the previous discussion gives a hint to construct a suitable multiplication in . Simply observe that

is a homeomorphism and so it is natural to define, for

It can be easily verified that it indeed is a compatible group structure. The above construction gives a recipe to define a compatible group structure to any topological space which is homeomorphic to another known to have a compatible group structure.

Now we modify the topological space a little bit and consider , the closure of . It turns out that the addition of two endpoints not only alters the topology, but also makes the new space void of any compatible group structure. The reader is encouraged to prove this fact and we will discuss it in the sequel.
The above example has told us that in order for topological spaces to have compatible group structures, some topological assumptions need to be imposed.

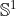
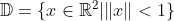
What if the topological space is a circle ? An open disk ? A cylinder ?

化長方為方、化三角為方

GRE前夕，不寫太詳細的Blog文。今天從鄭院長的網站見到兩條關於圓規直尺作圖的問題，在這裏以「高考純數卷」形式講講吧。中四或以上的學生已經有足夠的幾何常識，可嘗試逐part完成。

a) You are given a unit length (a line segment of length 1) and two segments with lengths x and y respectively. By considering two similar triangles, show that one can construct a segment with length xy.

b) You are given a unit length and a segment with length x. By considering a circle with diameter x+1, show that one can construct a segment with length .

c) "Quadrature" a plane figure means to construct a square where its area is equal to that of the plane figure, with use of straight edge and compasses only.

i) You are given a rectangle with sides x and y respectively. Show that you can quadrature the rectangle.

ii) You are given an arbitrary triangle. Show that you can quadrature the triangle. (Hint: by i), you should already know how to quadrature any given parallelogram.)

順帶一提，quadrature a given circle（即中文的「化圓為方」）是不可能做到的。

Poll statistics

Recently Terry Tao posted an interesting article at his blog that discusses some mathematics behind poll statistics. He proved (under some technical assumptions) that in a poll if p is the actual percentage of the whole population who vote yes and q is the percentage of people in a sample of the population who vote yes, then the probability that p and q differs by less than is at least



where n is the number of people in the sample. One of the key facts here is that the probability can be bounded by the absolute size of the sample (rather than the relative size with respect to the total population). Here's his original article:

http://terrytao.wordpress.com/2008/10/10/small-samples-and-the-margin-of-error/

A Nice Proof of "Infinite Primes of Form 4k+1"

Recently, I am writing a set of notes about prime numbers. Certainly I have included the most well-known fact about prime numbers in the set of notes --- there are infinitely many prime numbers. There are various proofs, including the most famous proof from Euclid.

I try to add something more into the set of notes. All prime numbers, except 2, have to be in the form of 4k+1 or 4k+3 (because all the other primes are odd). Two natural follow-up questions are, "Is there infinite number of primes of the form 4k+3?" and "Is there infinite number of primes of the form 4k+1?" The proof can be included in the set of notes as an appendix for more gifted students.

It turns out that the first question is easy to answer, by mimicking the technique from Euclid. If you have never heard this before, try to understand the proof by Euclid from the link above, and adopt the main idea to the "4k+3" question.

The second question, however, is more difficult. I am not sure if there is any simpler elementary solution, but I found a rather fascinating proof on web, using the Fermat's Little Theorem. Let me restate the proof here.

Given any integer N, consider , and p be the smallest prime factor of M.

Since 1, 2, ... , N all do not divide M, p is larger than N. Since p divides , we have



Taking -th power on both sides, we have

....(1)

On the other hand, by Fermat's Little Theorem, for a = 1, 2, ... , N, we have



Multiplying the above formula with a = 1, 2, ... , N, we get

....(2)

Comparing (1) and (2), we get



which implies is even and hence p is of the form 4k+1. As N is chosen arbitrarily, we reach the conclusion: there are infinitely many primes of the form 4k+1.

Is that too difficult for F.3 and F.4 students? I am not sure, but as it is put in the appendix, it is not demanding even I put the proof of Fermat's Last Theorem there. >.<""

0.999... = 1?

　　很多人應該在不少科普叢書或網上討論區見過「 = 1？」這問題。我們只需簡單的極限概念（甚至幾何級數和的概念），便知道這答案是肯定的， 等於 1。可是每當有人在討論區提出這問題時，答案總是似是而非，甚至出現很多不同的悖證。我不打算在這裏再證明一次這道命題，但卻想簡單闡釋以前見過的常見謬誤。

謬誤一：

　　 和 1 這兩個數的寫法不相同，它們怎可能一樣？

解釋：

　　我們先說明甚麼是小數。如果我們以小數形式寫成某實數 r 時，其表達式為 ，我們表示 ，其中 是整數部分，而 是第 n 個小數位。這是一個無窮項的和，因此我們求這個和時其實正在求某數列的極限。這個數列是 、、、、……。例如，我們指 時，其實指 是 、、、、……這數列的極限。

　　在這個定義裏，我們沒特別指明表示法是唯一的。換句話說，我們沒指出實數 r 不可以擁有兩種表達式 和 。這就好像兩個分數式 和 的值相同一樣。既然如此，為甚麼 不可以和 1 相同？

謬誤二：

　　我們不會將小數寫成以無窮個 9 結尾，因此 這寫法根本不成立。

解釋：

　　如果你接受 可以以無窮個 3 結尾，為甚麼無窮個 9 不可以？平日人們不會將 1 寫成 ，並不代表不可以這樣寫。　

謬誤三：

　　 的整數部分明明是 0，而 1 的整數部分是 1，為何它們會相同？

解釋：

　　請參看謬誤一。同一個實數可以擁有超過一種表示法。

謬誤四：

　　 只是非常接近 1，但不相同。

解釋：

　　請參看謬誤一。無窮小數的表達式是數列的極限。籠統地說，若一個數列 、、、……的極限是 L，則我們指當 n 愈來愈大時， 愈來愈接近 L。（當然這說法有點瑕疪，但極限的定義本來就依賴這想法而來。我們不在此深究這句子和極限的定義的分別。）以 為例，因為 、、、……這數列漸漸趨近 ，所以我們說 。我們指的是數列的極限是 ，而並非數列當中任何一項是 。如果你接受 ，為何不接受 = 1？