上個學期我改科大MATH202 (Introduction to Real Analysis) 的考試，最大得著是發現了兩件事：第一，原來很多學生不懂factorize 1- x^3；第二，原來有人還在用帶分數表示數值。
大家回想一下，你學分數時只是小三，當時老師是以切薄餅來解釋的。到了下學期，你終於儲夠錢買超過一個薄餅，於是老師便教你「帶分數」和「假分數」，而之前的分數被喚作「真分數」。
這不是很神奇嗎？少過一塊薄餅，怎樣切都是「真」的；超過一塊薄餅，你把它切開後，它就會成為「假」；當你保留完整的薄餅，再併上那些加埋不足一塊的剩餘物資，那就叫「帶」。那麼，這個「帶」，它就包含了完整與真實，但你把它重組，就會發現它虛假的本質。
但，做這樣的區別有意義嗎？當你上到中學、大學後，分數線上下的，都是甚麼 x-1 啊、e^x 的代數，你不知道她們實際上是甚麼數值，只知道她們的善變，於是真真假假，從此變得面目模糊。你小時候堅信那誓不兩立的真分數和假分數，已經分不開了。
唯獨帶分數這狡徒，他是真與假之間的賢者。你以為他已經棄世隱居了？不，在真假已沒有界線的塵世裡，他是一位入世的大隱士。當你要integrate (x+1)/(x-1) 時，他會告訴你：其實可以先化作 1 + 2/(x-1) 。嗟？豈非似曾相識？
2009年3月30日 星期一
2009年3月29日 星期日
小學集體回憶系列(1) 除號
各位大朋友，請問你上一次用除號是幾時的事？
除法，小二已經學到。除號，大家在小學時寫過千百次。
但你上到中學、大學後，基本上你是不會用除號的。反正把所有數都視為分數相乘，一條長得離譜的分數線就可以取代除號，就像日出時的地平線，上天下地一目了然，省卻了除號製造的混亂。
年紀跟我相約的朋友，上中學的年代正值電腦走入家庭。在鍵盤上除號更是無一席位，取而代之的是一個斜體的分數線" / "。當你要用電腦來打數式時，也會用equation editor附設的分數功能，而不會去找那個沒有歸宿的除號。
其實即使使用分數，乘號和" ... "都有其他用處。乘號在AL或大學可以表示cross multiplication，又或者，在每集的《全職獵人》開頭你會看到「乜乜X乜乜X乜乜」的標題，海報上也有「港樂X李克勤」的標題，就算是電玩也會有"藥水 X 3"、"手榴彈 X 5"的顯示。
至於代表餘數的" ... "，用途更厲害，只要你有用電腦同人溝通，無論是forum還是MSN，都一定會有" ... "。或者有點本末倒置，其實代表餘數只是她的兼職，她本來是一個沈默又猶豫的省略號。
除號是一位哀怨的宮娥，你曾經常常見到她，但你還未認識她，就已把她遺忘。
除法，小二已經學到。除號，大家在小學時寫過千百次。
但你上到中學、大學後，基本上你是不會用除號的。反正把所有數都視為分數相乘，一條長得離譜的分數線就可以取代除號，就像日出時的地平線，上天下地一目了然，省卻了除號製造的混亂。
年紀跟我相約的朋友，上中學的年代正值電腦走入家庭。在鍵盤上除號更是無一席位，取而代之的是一個斜體的分數線" / "。當你要用電腦來打數式時，也會用equation editor附設的分數功能，而不會去找那個沒有歸宿的除號。
其實即使使用分數，乘號和" ... "都有其他用處。乘號在AL或大學可以表示cross multiplication，又或者，在每集的《全職獵人》開頭你會看到「乜乜X乜乜X乜乜」的標題，海報上也有「港樂X李克勤」的標題，就算是電玩也會有"藥水 X 3"、"手榴彈 X 5"的顯示。
至於代表餘數的" ... "，用途更厲害，只要你有用電腦同人溝通，無論是forum還是MSN，都一定會有" ... "。或者有點本末倒置，其實代表餘數只是她的兼職，她本來是一個沈默又猶豫的省略號。
除號是一位哀怨的宮娥，你曾經常常見到她，但你還未認識她，就已把她遺忘。
小學集體回憶系列(前言)
眼見現在小學課程越改越亂，我不由得回想起小學時代那顯淺而深刻的「填鴨料」。舊制下的小學課程雖然不太重視思維，但所學的全都是實用且概念明確。
有些知識老師是教過，被視為「基礎知識」，於是一直都沒有加以討論、證明、理解。
有些知識被視為真理，你後來卻發覺根本就不是那回事。
有些技巧大家花了很多時間去學，但當你讀上去時卻發覺一無是處。
有些行為被視為禁忌，你長大後卻發現原來可以無視它們。
有些行為被視為規條，你長大後卻對它們念念不忘。
在純真的回憶裡，讓我們回到我們的歲月！
有些知識老師是教過，被視為「基礎知識」，於是一直都沒有加以討論、證明、理解。
有些知識被視為真理，你後來卻發覺根本就不是那回事。
有些技巧大家花了很多時間去學，但當你讀上去時卻發覺一無是處。
有些行為被視為禁忌，你長大後卻發現原來可以無視它們。
有些行為被視為規條，你長大後卻對它們念念不忘。
在純真的回憶裡，讓我們回到我們的歲月！
2009年3月28日 星期六
2009 + 1 = ?
看下去之前，先想想：2009 + 1 = ?
踏入 2009 年後，很多數學題的主角都換成了 2009，而很多時在計算的過程中都不免要把「主角」加上 1。我已經遇過很多次，學生認為 2009 + 1 等於 3000。研究心理學的朋友，這個應該是個不錯的研究課題。
踏入 2009 年後，很多數學題的主角都換成了 2009，而很多時在計算的過程中都不免要把「主角」加上 1。我已經遇過很多次，學生認為 2009 + 1 等於 3000。研究心理學的朋友，這個應該是個不錯的研究課題。
2009年3月24日 星期二
2009年3月20日 星期五
Cylindrical projection, an Archimedes' result, and Duistermaat-Heckman Theorem
I am always amazed by how accurately some old world map made long time ago depicted the globe. Cartography, or simply map-making, has long been an established form of art and science since navigation to the New World became more and more active. There are several cartography techniques which serve to describe certain geometrical information of the world geography. Cylindrical projection is one of them.
The principle of cylindrical projection is simple indeed. Let us imagine that the globe is a perfect sphere which is inscribed in a cylinder with its height and radius of cross section equal to the radius of the globe. Position this geometric configuration in the three dimensional coordinate system in such a way that the
-axis passes through the center of both the sphere and the cross section of the cylinder. Cylindrical projection is just the horizontal radial projection from the sphere onto the curved surface of the cylinder. Put in a more mathematical way, cylindrical projection maps a point with -coordinate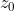 
to the intersection of the cylindrical surface and the horizontal ray(parallel to the 
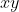-plane) emanating from )
and passing through that point.
World maps made by cylindrical projection is obtained by flattening out the image of cylindrical projection on the cylindrical surface. For the convenience of archiving, it has been more common to draw world maps on a flat sheet of paper than on a sphere. But paper maps have one major drawback--they greatly distort the actual geography of the world. More precisely, distances on any paper map are not proportional to actual distances. This is a simple consequence of Gauss's Theorema Egregium, which states that the Gaussian curvature of any surface is expressible in terms of its metric. Since a sphere has constant positive curvature, whereas a plane has vanishing curvature, there is no map between them preserving distance. You may observe that the closer to the Poles a place is, the more distortedly it is presented on a map made by cylindrical projection. For instance, the Antarctica appears to be much more elongated on such maps.
But cylindrical projection is not completely without any merit. In fact cylindrical projection is area-preserving. Legend has it that this result was discovered to Archimedes. It is rather mysterious to me how Archimedes derived this fact. Anyway I will show below a proof which amounts to a 'change of variables', but is rephrased in differential-form terminology.
It suffices to show that the cylindrical projection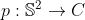
induces a pullback 
which maps the area form of the cylinder to that of the inscribed sphere. The spherical coordinates are
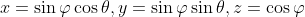
whereas the cylindrical coordinates are
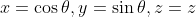
So=(\theta, \cos\varphi))
. Note that the area form of the sphere is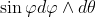 
, while that of the cylinder is 
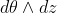. Its pullback by 
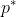is
=d\theta\wedge d(\cos\varphi)=d\theta\wedge (-\sin\varphi d\varphi)=\sin\varphi d\varphi\wedge d\theta)
So we are done.
For those who enjoy understanding math from a vantage point of view, note that this result of Archimedes' turns out to be a particular case of a theorem in symplectic geometry known as Duistermaat-Heckman Theorem. It says that given a Hamiltonian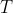
-space )
where 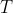is a torus and 
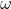the symplectic form of 
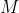, then the Radon-Nikodym derivative of the pushforward of the canonical measure (given by 
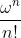, 2n=dimensional of 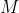) through the moment map 
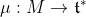with respect to the Lebesgue measure of 
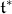is piecewise polynomial, i.e. for any measurable 
,
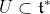}\frac{\omega^n}{n!}=\int_U p(t)dt)
for some piecewise polynomial )
in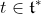 
. Here the sphere is a Hamiltonian 
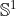-space, where its symplectic form is just the area form, 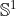acts on the sphere by rotating about the vertical axis at unit speed and the moment map is the height function. The Radon-Nikodym derivative in this case is the constant 
.
The principle of cylindrical projection is simple indeed. Let us imagine that the globe is a perfect sphere which is inscribed in a cylinder with its height and radius of cross section equal to the radius of the globe. Position this geometric configuration in the three dimensional coordinate system in such a way that the
World maps made by cylindrical projection is obtained by flattening out the image of cylindrical projection on the cylindrical surface. For the convenience of archiving, it has been more common to draw world maps on a flat sheet of paper than on a sphere. But paper maps have one major drawback--they greatly distort the actual geography of the world. More precisely, distances on any paper map are not proportional to actual distances. This is a simple consequence of Gauss's Theorema Egregium, which states that the Gaussian curvature of any surface is expressible in terms of its metric. Since a sphere has constant positive curvature, whereas a plane has vanishing curvature, there is no map between them preserving distance. You may observe that the closer to the Poles a place is, the more distortedly it is presented on a map made by cylindrical projection. For instance, the Antarctica appears to be much more elongated on such maps.
But cylindrical projection is not completely without any merit. In fact cylindrical projection is area-preserving. Legend has it that this result was discovered to Archimedes. It is rather mysterious to me how Archimedes derived this fact. Anyway I will show below a proof which amounts to a 'change of variables', but is rephrased in differential-form terminology.
It suffices to show that the cylindrical projection
whereas the cylindrical coordinates are
So
For those who enjoy understanding math from a vantage point of view, note that this result of Archimedes' turns out to be a particular case of a theorem in symplectic geometry known as Duistermaat-Heckman Theorem. It says that given a Hamiltonian
2009年3月9日 星期一
Convolution Technique in Generating Function (1)
When I was the TA of the course "Combinatorial Analysis" in HKUST, I told students that one of the powerful properties of generating function is "convolution".
(*)To combinatorially construct an object of size n, it is a common way to first construct two smaller objects of size k and M-k (where M is a function of n, say, n or (n-1)), and then join the two smaller objects together.
The most famous example must be finding the Catalan Number. Catalan Number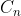
is counting the number of ways to write n "+1" and n "-1" in a row such that the for 
, the sum of the first k terms (we denote it by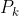 
) is NOT negative. For example, when 
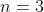, "+1 +1 -1 -1 +1 -1" and "+1 +1 +1 -1 -1 -1" satisfy the requirement while "+1 +1 -1 -1 -1 +1" does not (the first five terms sum to -1, which is negative).
Now we find out a recurrence of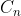 using the technique mentioned in (*). We denote the ith term be 
.
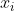You know,
and 
. So there exists a smallest 
such that 
. (
is impossible if a is odd.)
The terms between
and 
(inclusive) must itself form a Catalan sequence of size 2k. The reason is, if it is not a Catalan sequence, then 
for some 
, and then , 
, i.e. contradicting to the assumption that k is the smallest integer such that 
. Hence, there are 
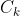ways to fill in to .
Similarly, the terms between
and 
(inclusive) must itself form a Catalan sequence of size 2n-2k-2. Hence, there are 
ways to fill in to .
Hence, if k is the smallest integer such that, there are 
ways to construct a Catalan sequence of size 2n. The value of k can be varied from 0 to n-1. So we have the "convolution recurrence":
Now define the generating function
. Reader can check that (by comparing coefficients)
This is what we called "convolution" in the first paragraph. When someone multiplies two polynomials, to find the coefficient of
, he has to multiply the term 
in the first polynomial to the term 
in the second polynomial. This "one increase, one decrease" property for polynomial multiplication gives the great convenience for the generating function to handle the convolution recurrence for Catalan numbers.
Now, the remaining task is purely algebraic. For, treat 
as a variable, then it becomes a quadratic equation. By quadratic formula, we have
Requiring has no pole at 
, we reject 
and hence
Lastly, apply Newton's binomial theorem to
, we arrive at the fact that
(*)To combinatorially construct an object of size n, it is a common way to first construct two smaller objects of size k and M-k (where M is a function of n, say, n or (n-1)), and then join the two smaller objects together.
The most famous example must be finding the Catalan Number. Catalan Number
Now we find out a recurrence of
You know,
The terms between
Similarly, the terms between
Hence, if k is the smallest integer such that
Now define the generating function
This is what we called "convolution" in the first paragraph. When someone multiplies two polynomials, to find the coefficient of
Now, the remaining task is purely algebraic. For
Requiring
Lastly, apply Newton's binomial theorem to
訂閱：
文章 (Atom)