證明方程 x4 - 8x3 + 22x2 - 24x + 10 = 0 沒有實根。
2008年6月27日 星期五
2008年6月21日 星期六
2008年6月20日 星期五
托運行李箱
小弟將移居西雅圖，有超多物品要由香港搬走。由於想盡量托運多些行李，故特意於兩間售賣行李箱的店舖逛逛，搜集了一些第一手資料：
1 號行李箱 : 12 x 21 x 30 吋
2 號行李箱 : 10 x 18 x 26 吋
3 號行李箱 : 11 x 20 x 30 吋
4 號行李箱 : 9 x 15 x 23 吋
5 號行李箱 : 12 x 19 x 29 吋
6 號行李箱 : 11 x 16 x 25 吋
航空公司托運行李的限額是：
每人免費托運兩件各重 23 公斤的行李 (四月中前是 32 公斤的!!)
兩件長闊高之總和不可超過 107 吋，其中一件長闊高之和不可超過 62 吋。
要買那(兩)個行李箱，才可托運最多行李？朋友覺得「買兩個一樣大的中型行李箱」 比 「買一個大和一個小」 好，你認為如何？
--------------------------------------------------------------------------
設 x, y, z 是第一個行李箱的尺寸，a, b, c 是第二個行李箱的尺寸。不妨假設 x+y+z >= a+b+c 。若只考慮體積，以上問題是
用 AM-GM 不等式，我們知道取得最大值時， x=y=z 且 a=b=c 。(為什麼沒有 Cube 形的行李箱 ga! T口T~~~ 如果大家知道哪裡有一些近似 Cube 的行李箱，煩請告知。不勝感激!)
經過計算，最大值當且僅當 x=y=z=62/3 和 a=b=c=45/3 時成立，且答案是 12201.963 (準確至小數點後 3 位) 。大家不妨驗證。 換句話說，若只考慮體積，「買一個大型行李箱和一個小型行李箱」 比 「買兩個一樣大的中型行李箱」好。
暫時我的方案是：買 2 號和 5 號行李箱，5 號裝一些較輕的東西，2 號裝一些較重的東西。(希望航空公司不會檢查長闊高，查的話即場把 2 號換成一個更小的行李箱，心痛地放棄部分書本)。
1 號行李箱 : 12 x 21 x 30 吋
2 號行李箱 : 10 x 18 x 26 吋
3 號行李箱 : 11 x 20 x 30 吋
4 號行李箱 : 9 x 15 x 23 吋
5 號行李箱 : 12 x 19 x 29 吋
6 號行李箱 : 11 x 16 x 25 吋
航空公司托運行李的限額是：
每人免費托運兩件各重 23 公斤的行李 (四月中前是 32 公斤的!!)
兩件長闊高之總和不可超過 107 吋，其中一件長闊高之和不可超過 62 吋。
要買那(兩)個行李箱，才可托運最多行李？朋友覺得「買兩個一樣大的中型行李箱」 比 「買一個大和一個小」 好，你認為如何？
--------------------------------------------------------------------------
設 x, y, z 是第一個行李箱的尺寸，a, b, c 是第二個行李箱的尺寸。不妨假設 x+y+z >= a+b+c 。若只考慮體積，以上問題是
已知 x+y+z+a+b+c <= 107 ，且 x+y+z <= 62 ，求 xyz+abc 的最大值。
用 AM-GM 不等式，我們知道取得最大值時， x=y=z 且 a=b=c 。(為什麼沒有 Cube 形的行李箱 ga! T口T~~~ 如果大家知道哪裡有一些近似 Cube 的行李箱，煩請告知。不勝感激!)
經過計算，最大值當且僅當 x=y=z=62/3 和 a=b=c=45/3 時成立，且答案是 12201.963 (準確至小數點後 3 位) 。大家不妨驗證。 換句話說，若只考慮體積，「買一個大型行李箱和一個小型行李箱」 比 「買兩個一樣大的中型行李箱」好。
暫時我的方案是：買 2 號和 5 號行李箱，5 號裝一些較輕的東西，2 號裝一些較重的東西。(希望航空公司不會檢查長闊高，查的話即場把 2 號換成一個更小的行李箱，心痛地放棄部分書本)。
2008年6月19日 星期四
A "Football Theorem"
With the European Football Championship being a hot topic these days (this is especially true for me as I am now in a country that is crazy about the sport!), let me share with you a theorem about football. It goes like this:
"Place the ball in the center of the court, and start the game. The next time when the ball is being placed at the center of the court again, there exists one point on the ball which is at exactly the same position as it was in the first time."
The proof only involves a simple concept in elementary Linear Algebra, so do think before looking at the hint below!
Highlight the space in the right for the hint: Use the fact that every rotation has an eigenvalue 1.
"Place the ball in the center of the court, and start the game. The next time when the ball is being placed at the center of the court again, there exists one point on the ball which is at exactly the same position as it was in the first time."
The proof only involves a simple concept in elementary Linear Algebra, so do think before looking at the hint below!
Highlight the space in the right for the hint: Use the fact that every rotation has an eigenvalue 1.
2008年6月17日 星期二
"Generalize"的雜談（一）
唸了數學多年，其實數學上很多問題都是源自數學家對問題或解法的generalizaion。
舉一個大部分中學生都明白的例子。在我還是讀小學的時候，我聽過了Gauss怎樣用巧妙的方法計算 1+2+3+...+100的值。還記得嗎？他的做法就是把數式倒轉寫一次：
1 + 2 + 3 + ... + 100
100+ 99 + 98 + ... + 1
然後發現一上一下的兩個數和都是101。而這裏有100對，所以總和是101 * 100 = 10100。因為算式總共加了兩次，所以答案是5050。這種配對（pairing）的方法，在現時的奧數訓練可謂必修，但並不一定用在計數列之上。在組合數學中，配對也是一種常用的方法；組合數學裏的這個方法被給了一個名稱：一一對應。這樣可以說是一種解法的generalization。
第一段說了有問題和解法的generalization。解法的generalization上一段已經給了一個例子。而問題的generalization呢？例子多的是。有讀附加數的學生在讀數學歸納法（Mathematical Induction）時，一定對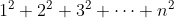
的公式不陌生。但你們有沒有想過，那個已經給了你的
別人是怎樣求出來的？進一步可以問：當
時，
有沒有"closed form"呢？這就是最簡單對問題的generalization：當解決了一個「細數字」的問題時，考慮一下「大數字」的問題。
有些時候，我們可以從「細數字問題」的解題中看到解決「大數字問題」的竅門。但上面這個問題，配對這個方法並行不通；這個時候就是數學家研究出其他方法的show time。好像上一段的問題，原來可以輕易地用binomial theorem解決；而且，對於任何 k 的方法都是類似的。
不過並不是所有「大數字問題」都可從「細數字問題」的題解中偷師。數學歷史上甚至出現過一個問題，它的二維、四維、五維、六維等打後的情況在很早就被解決，唯獨是三維的情況卻非常困難，甚至考起了數學家足足200年之久。這就是著名的龐卡萊猜想（Poincare conjecture）了。
說起維數的generalization，得說說一個數學笑話。有說一個數學家叫A. Coble，做代數幾何的，據稱他有無窮個博士論文的題目。當一個博士生解決了問題的二維情況時，他就叫下一個博士生做三維情況，再叫下下一個博士生做四維情況。後來有一個叫Gerald Huff的人，不但解決了五維情況，而其他更大維數的情況也解決了。這讓A. Coble未來的博士學生無所事事。這令A. Coble很怒……
舉一個大部分中學生都明白的例子。在我還是讀小學的時候，我聽過了Gauss怎樣用巧妙的方法計算 1+2+3+...+100的值。還記得嗎？他的做法就是把數式倒轉寫一次：
1 + 2 + 3 + ... + 100
100+ 99 + 98 + ... + 1
然後發現一上一下的兩個數和都是101。而這裏有100對，所以總和是101 * 100 = 10100。因為算式總共加了兩次，所以答案是5050。這種配對（pairing）的方法，在現時的奧數訓練可謂必修，但並不一定用在計數列之上。在組合數學中，配對也是一種常用的方法；組合數學裏的這個方法被給了一個名稱：一一對應。這樣可以說是一種解法的generalization。
第一段說了有問題和解法的generalization。解法的generalization上一段已經給了一個例子。而問題的generalization呢？例子多的是。有讀附加數的學生在讀數學歸納法（Mathematical Induction）時，一定對
有些時候，我們可以從「細數字問題」的解題中看到解決「大數字問題」的竅門。但上面這個問題，配對這個方法並行不通；這個時候就是數學家研究出其他方法的show time。好像上一段的問題，原來可以輕易地用binomial theorem解決；而且，對於任何 k 的方法都是類似的。
不過並不是所有「大數字問題」都可從「細數字問題」的題解中偷師。數學歷史上甚至出現過一個問題，它的二維、四維、五維、六維等打後的情況在很早就被解決，唯獨是三維的情況卻非常困難，甚至考起了數學家足足200年之久。這就是著名的龐卡萊猜想（Poincare conjecture）了。
說起維數的generalization，得說說一個數學笑話。有說一個數學家叫A. Coble，做代數幾何的，據稱他有無窮個博士論文的題目。當一個博士生解決了問題的二維情況時，他就叫下一個博士生做三維情況，再叫下下一個博士生做四維情況。後來有一個叫Gerald Huff的人，不但解決了五維情況，而其他更大維數的情況也解決了。這讓A. Coble未來的博士學生無所事事。這令A. Coble很怒……
2008年6月14日 星期六
MD Academic Seminar June 2008
今個月MD又開會，之後亦一如以往，有academic seminar；詳情如下：
題目：準確傳送的秘密－－編碼學
TOPIC: The Secret of Accurate Transmission - Coding Theory
講者：陳鍵行先生（University of Illinois at Chicago）
SPEAKER: Mr Andy Chan (University of Illinois at Chicago)
日期：2008年6月21日（星期六）
DATE: June 21, 2008 (Sat)
時間：下午五時至下午六時十五分
TIME: 5pm--6:15pm
地點：香港城市大學 P4909 室（紫色區域四樓）
VENUE: Room P4909 (Purple Zone, 4/F) in City University of Hong Kong
歡迎任何對數學有興趣的人來聽講座。
Anyone who are interested in Mathematics are welcomed to this seminar.
************************************************************************************************************************
準確傳送的秘密－－編碼學
現代資訊交流頻繁。簡單至手填表格，複雜至電腦以光纖傳送資料都是生活不可或缺的部分。我們可以怎樣利用數學減少傳遞訊息時出錯的機會？方法就是編碼學。講座將討論幾種常用的測錯和除錯方法，並簡介其背後的數學結構。
The Secret of Accurate Transmission - Coding Theory
Data transfer is frequent nowadays. It plays an important role in our daily life. It can be as simple as filling forms manually, or as complicated as data transmission between computers via optical fibres. How can we reduce errors during the course of transmission with mathematics? The method is coding theory! In the seminar, we will discuss several error-detecting and error-correcting methods. The mathematical structure behind will be introduced as well.
-------------------------------------------------------------------
講座流程：
1. 編碼學的用途
2. 最基本的例子：重覆編碼
3. 最常見的例子：檢測碼
4. 測錯距離及除錯距離
5. Hamming 碼
題目：準確傳送的秘密－－編碼學
TOPIC: The Secret of Accurate Transmission - Coding Theory
講者：陳鍵行先生（University of Illinois at Chicago）
SPEAKER: Mr Andy Chan (University of Illinois at Chicago)
日期：2008年6月21日（星期六）
DATE: June 21, 2008 (Sat)
時間：下午五時至下午六時十五分
TIME: 5pm--6:15pm
地點：香港城市大學 P4909 室（紫色區域四樓）
VENUE: Room P4909 (Purple Zone, 4/F) in City University of Hong Kong
歡迎任何對數學有興趣的人來聽講座。
Anyone who are interested in Mathematics are welcomed to this seminar.
************************************************************************************************************************
準確傳送的秘密－－編碼學
現代資訊交流頻繁。簡單至手填表格，複雜至電腦以光纖傳送資料都是生活不可或缺的部分。我們可以怎樣利用數學減少傳遞訊息時出錯的機會？方法就是編碼學。講座將討論幾種常用的測錯和除錯方法，並簡介其背後的數學結構。
The Secret of Accurate Transmission - Coding Theory
Data transfer is frequent nowadays. It plays an important role in our daily life. It can be as simple as filling forms manually, or as complicated as data transmission between computers via optical fibres. How can we reduce errors during the course of transmission with mathematics? The method is coding theory! In the seminar, we will discuss several error-detecting and error-correcting methods. The mathematical structure behind will be introduced as well.
-------------------------------------------------------------------
講座流程：
1. 編碼學的用途
2. 最基本的例子：重覆編碼
3. 最常見的例子：檢測碼
4. 測錯距離及除錯距離
5. Hamming 碼
2008年6月9日 星期一
百年一遇
Just read the following article from Mingpao. You'll know right away why I'm sharing it here. :p
明年再逢百年一雨機率不減 2008年6月9日
【明報專訊】前日一場「百年一遇」大雨，令香港多處成澤國，不過，「百年一遇」大雨今年已過，不等於明年沒有，因為明年出現的機率與今年一樣；加上「重遇期」可適用於不同地方，故同年內不同地區都有可能發生「X年一遇」的大雨。
在統計學上，地震、颱風及暴雨等自然現象都是隨機發生的事件，但經過分析，就可計算出「重遇期」，代表重複發生同一事件的平均所需時間。發生百年一遇大雨後，今年再發生的機會率低於百分之一，但明年再發生的機會率仍是百分之一。
即使「百年一遇」事件的重遇周期是100年，並不代表每百年才發生一次，因為「重遇期」可適用於不同地方，在香港，不同地區的雨量可以有很大出入，故同一年內不同地區亦有可能發生過「X年一遇」的大雨。
除地點外，下雨時間長短亦可形成「X年一遇」大雨，有時是1小時的「X年一遇」大雨，有時是兩小時的「X年一遇」大雨。降雨速度、密度及時間有分別，對不同地區造成的影響亦有分別，因此，不可單看「X年一遇」大雨，便一概而論破壞力有多大。
明年再逢百年一雨機率不減 2008年6月9日
【明報專訊】前日一場「百年一遇」大雨，令香港多處成澤國，不過，「百年一遇」大雨今年已過，不等於明年沒有，因為明年出現的機率與今年一樣；加上「重遇期」可適用於不同地方，故同年內不同地區都有可能發生「X年一遇」的大雨。
在統計學上，地震、颱風及暴雨等自然現象都是隨機發生的事件，但經過分析，就可計算出「重遇期」，代表重複發生同一事件的平均所需時間。發生百年一遇大雨後，今年再發生的機會率低於百分之一，但明年再發生的機會率仍是百分之一。
即使「百年一遇」事件的重遇周期是100年，並不代表每百年才發生一次，因為「重遇期」可適用於不同地方，在香港，不同地區的雨量可以有很大出入，故同一年內不同地區亦有可能發生過「X年一遇」的大雨。
除地點外，下雨時間長短亦可形成「X年一遇」大雨，有時是1小時的「X年一遇」大雨，有時是兩小時的「X年一遇」大雨。降雨速度、密度及時間有分別，對不同地區造成的影響亦有分別，因此，不可單看「X年一遇」大雨，便一概而論破壞力有多大。
2008年6月6日 星期五
數學習慣
通常真正的數學人總會有一些奇怪的數學習慣。
小時對數字的觸覺很敏感。打從小四（還是小五？）學了怎樣判斷一個數是否9的倍數的方法後，已經自己參透了一個數除9的餘數和數字和除9的餘數是一樣的。於是，在街上走著，一見到一些數字，例如車牌、電話，就會心算這些數字除9的餘數。
因為只需計算數字和除9的餘數，所以當見到數字當中有9或一些和是9的倍數的數字，就可以不理，在心裏面算行刪去——好像見到「1、2、6」、「7、7、4」等。問題來了：有電話號碼是不可以使用這個技巧的嗎？
例子是有的，例如11111111、44444444等（不過這些似乎都不是香港登記的電話號碼；題外話，以前有一個無聊的鬼故，說夜晚打電話不斷按1，會駁通到陰曹地府……不過這仍然不是香港登記的電話號碼。）。香港的電話號碼都是8位數，有興趣的人可以想想，除了8個連續一樣的數字外，還有別的數字是不可以使用第二段提過的技巧加快運算嗎？
小時對數字的觸覺很敏感。打從小四（還是小五？）學了怎樣判斷一個數是否9的倍數的方法後，已經自己參透了一個數除9的餘數和數字和除9的餘數是一樣的。於是，在街上走著，一見到一些數字，例如車牌、電話，就會心算這些數字除9的餘數。
因為只需計算數字和除9的餘數，所以當見到數字當中有9或一些和是9的倍數的數字，就可以不理，在心裏面算行刪去——好像見到「1、2、6」、「7、7、4」等。問題來了：有電話號碼是不可以使用這個技巧的嗎？
例子是有的，例如11111111、44444444等（不過這些似乎都不是香港登記的電話號碼；題外話，以前有一個無聊的鬼故，說夜晚打電話不斷按1，會駁通到陰曹地府……不過這仍然不是香港登記的電話號碼。）。香港的電話號碼都是8位數，有興趣的人可以想想，除了8個連續一樣的數字外，還有別的數字是不可以使用第二段提過的技巧加快運算嗎？
2008年6月1日 星期日
Investigating lengths and areas
Inspired by Kahoo, who wrote an article on some possible investigations that a primary school student can carry out of the Fibonacci sequence, let me also try posting some questions in geometry, so that some of you may try your hands on them. (Unfortunately I think the questions that follow will require knowledge from high school mathematics :p)
Suppose we are given a rope of length L.
1. What is the area of the largest rectangle that one can enclose using the given rope?
Do you have any intuition about this problem? Let's try some extreme cases. A rectangle of a given perimeter L is determined by its length, which can vary from 0 to L/2. Suppose we are in these extreme cases. What would the areas of the rectangles be? Suppose we gradually move from one extreme to another. What will happen to the area of the rectangle? Does that give you some intuition, and suggest how you could prove it?
Students who know one-variable calculus can solve this as a maximization problem; students who does not know calculus can solve it by some simple algebra (for instance, using the difference of squares formula, which is essentially the essence of the calculus method).
Graduate students in mathematics can also do this by flowing the rectangle into a square :p
2. What is the area of the largest triangle that one can enclose using the given rope?
A triangle with given perimeter is determined by 2 parameters (e.g. the length of two of its sides). So this would look like a two-dimensional maximization problem. Students who know multi-variable calculus can solve this by invoking Heron's formula. What if you don't know two-variable calculus? Is there a way of reducing the problem to one-variable?
The answer is yes, provided that you know the maximum exists in the first place: then look at the configuration for which the area of the triangle is a maximum, fixing one of the sides and vary the other two, one realizes (using one-variable calculus now, because the length of one of the variable sides determines the length of the other!) that the two variable sides have the same length. This would show indeed that the maximum can only be achieved when the lengths of all three sides of the triangle are the same, i.e. when it is an equilateral triangle.
Actually a simple geometric symmetry argument already leads to the above observation, and one can bypass calculus altogether!
3. What is the area of the largest shape that one can enclose using the given rope? (This is the famous isoperimetric inequality.)
First, what is the intuition?
Now that the shape of the enclosed area is arbitrary, we have an infinite degree of freedom when we maximize the area; indeed if one formulates the problem correctly, one can do a maximization involving only "countably many variables". For instance, check out the following two Fourier analytic proofs of the isoperimetric inequality in The everything seminar, that makes use of the Fourier series of nice periodic functions.
I'm also thinking that maybe one can also prove the isoperimetric inequality using calculus of variations (an infinitely many variable version of calculus). Any suggestions?
4. Can the problem be further generalized?
Sure, how about a higher dimensional version of the isoperimetric problem?
As it turns out, the isoperimetric problem is closely related to some other important inequalities in analysis, like the Sobolev inequalities (say for smooth functions with compact supports)
|^{\frac{n}{n-1}}dx\right)^{\frac{n-1}{n}} \leq C_n \int_{\mathbb{R}^n}|\nabla f(x)|dx)
(which allows one to control the size of a function from its derivatives).
Suppose we are given a rope of length L.
1. What is the area of the largest rectangle that one can enclose using the given rope?
Do you have any intuition about this problem? Let's try some extreme cases. A rectangle of a given perimeter L is determined by its length, which can vary from 0 to L/2. Suppose we are in these extreme cases. What would the areas of the rectangles be? Suppose we gradually move from one extreme to another. What will happen to the area of the rectangle? Does that give you some intuition, and suggest how you could prove it?
Students who know one-variable calculus can solve this as a maximization problem; students who does not know calculus can solve it by some simple algebra (for instance, using the difference of squares formula, which is essentially the essence of the calculus method).
Graduate students in mathematics can also do this by flowing the rectangle into a square :p
2. What is the area of the largest triangle that one can enclose using the given rope?
A triangle with given perimeter is determined by 2 parameters (e.g. the length of two of its sides). So this would look like a two-dimensional maximization problem. Students who know multi-variable calculus can solve this by invoking Heron's formula. What if you don't know two-variable calculus? Is there a way of reducing the problem to one-variable?
The answer is yes, provided that you know the maximum exists in the first place: then look at the configuration for which the area of the triangle is a maximum, fixing one of the sides and vary the other two, one realizes (using one-variable calculus now, because the length of one of the variable sides determines the length of the other!) that the two variable sides have the same length. This would show indeed that the maximum can only be achieved when the lengths of all three sides of the triangle are the same, i.e. when it is an equilateral triangle.
Actually a simple geometric symmetry argument already leads to the above observation, and one can bypass calculus altogether!
3. What is the area of the largest shape that one can enclose using the given rope? (This is the famous isoperimetric inequality.)
First, what is the intuition?
Now that the shape of the enclosed area is arbitrary, we have an infinite degree of freedom when we maximize the area; indeed if one formulates the problem correctly, one can do a maximization involving only "countably many variables". For instance, check out the following two Fourier analytic proofs of the isoperimetric inequality in The everything seminar, that makes use of the Fourier series of nice periodic functions.
I'm also thinking that maybe one can also prove the isoperimetric inequality using calculus of variations (an infinitely many variable version of calculus). Any suggestions?
4. Can the problem be further generalized?
Sure, how about a higher dimensional version of the isoperimetric problem?
As it turns out, the isoperimetric problem is closely related to some other important inequalities in analysis, like the Sobolev inequalities (say for smooth functions with compact supports)
(which allows one to control the size of a function from its derivatives).
訂閱：
文章 (Atom)