最近在科大旁聽functional analysis,偶然會聽到一些數學的歷史故事。
有一個叫Lomonosov的人,在俄羅斯讀大學,上課時遲到,去到課室時教授和學生們都走了,只見到兩塊黑板上,第一塊寫住一條問題,而另一塊則寫著一些topology關於fixed points的定理。Lomonosov也不管三七廿一,把這些東西都抄到筆記裏。他以為那條問題是教授給的功課,於是開始努力想著。最後,他用了那些關於fixed points的定理解決了。
下一堂,他把題解交給教授。但……
其實那條問題是一條幾十年未有人破的open problem,當時教授只是寫在黑板上說這是open problem。而另一塊黑板關於fixed points的定理,其實是再對上一堂另一個教授教書時寫的……
2008年4月29日 星期二
2008年4月24日 星期四
數學雜記
1)
某日和Adam上堂時突然說起課程改革。
Adam:「不如索性將數學呢科cut左佢啦。」
我:「都啱。好過而家被人強暴。」
說笑罷了。數學當然要留。
上星期TVB播《霍元甲》,田中安野對霍元甲說:「活著比甚麼都重要。」
霍元甲回應:「活著,從來都不是一個人的事。」
不知道你們明不明白我上一段的意思了。
2)
暫時香港大概有三個數學blogs,就是「數學真魅」、「Quod Erat Demonstrandum」和本手記。(有沒有其他的數學網誌?歡迎提供。)最近見到「數學真魅」的主持上了有線電視接受訪問。(其實不知道是多久前,總是是近兩日才見到YouTube有。)在此轉播一下吧。
某日和Adam上堂時突然說起課程改革。
Adam:「不如索性將數學呢科cut左佢啦。」
我:「都啱。好過而家被人強暴。」
說笑罷了。數學當然要留。
上星期TVB播《霍元甲》,田中安野對霍元甲說:「活著比甚麼都重要。」
霍元甲回應:「活著,從來都不是一個人的事。」
不知道你們明不明白我上一段的意思了。
2)
暫時香港大概有三個數學blogs,就是「數學真魅」、「Quod Erat Demonstrandum」和本手記。(有沒有其他的數學網誌?歡迎提供。)最近見到「數學真魅」的主持上了有線電視接受訪問。(其實不知道是多久前,總是是近兩日才見到YouTube有。)在此轉播一下吧。
2008年4月21日 星期一
Helly's selection theorem
Yesterday a friend of mine showed me a very cute and completely elementary fact about convex sets in the plane, and perhaps I could share it here. It's a classical theorem due to Helly. It actually works in arbitrarily high dimensions, but for clarity of exposition let's restrict ourselves to the Euclidean plane 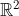 . The theorem is the following:
. The theorem is the following:
You may wish to draw a picture to convince yourself of this theorem before proceeding.
The proof is based on the following lemma:
(If some of you are not familiar with the notions used in the above statement, here is another (more clumsy) way of saying the same thing: Let be any 4 points in the plane. Then one can find a set of labels
be any 4 points in the plane. Then one can find a set of labels 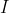 , consisting of some of the numbers 1, 2, 3 and 4, such that the following is true: Let
, consisting of some of the numbers 1, 2, 3 and 4, such that the following is true: Let  be the collection of points
be the collection of points 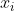 whose label
whose label 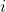 is in
is in 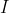 , and let
, and let  be the collection of the remaining points. Let
be the collection of the remaining points. Let  be the smallest convex set containing all the points in
be the smallest convex set containing all the points in  , and
, and  be the smallest convex set containing all the points in
be the smallest convex set containing all the points in  . Then the two sets
. Then the two sets  and
and  contain a common point.)
contain a common point.)
The proof of the lemma is based on the following linear algebra argument:
Consider the system of 3 linear equations in 4 unknown real numbers :
:


(The second equation is a vector equation in the plane, so it actually represents two linear equations.)
A well-known linear algebra fact is that if you have 3 linear equations in 4 unknowns, you can always find a non-zero solution to the equation. Suppose by abuse of notation is such a solution. By relabelling the points if necessary, we can assume that there is a certain label
is such a solution. By relabelling the points if necessary, we can assume that there is a certain label 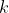 such that
such that  are all positive while
are all positive while  are all less than or equal to 0.
are all less than or equal to 0.
Now from the first defining equation of , we have
, we have
 .
.
Since we assumed is a non-zero solution, the quantity on the left hand side of the above equation must be positive. Let's call it
is a non-zero solution, the quantity on the left hand side of the above equation must be positive. Let's call it  .
.
From the second defining equation of , we have
, we have
 .
.
Dividing both sides of the equation by , we get
, we get
 .
.
But the left hand side of this equation is a convex linear combination of the points , and hence is in the convex hull of
, and hence is in the convex hull of  ; similarly the right hand side of the equation is in the convex hull of
; similarly the right hand side of the equation is in the convex hull of  . This completes the proof of the lemma.
. This completes the proof of the lemma.
Next, we shall prove the theorem by induction on the number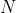 of convex sets involved. The theorem is of course trivial if
of convex sets involved. The theorem is of course trivial if  . Suppose now the theorem has been proved for a certain
. Suppose now the theorem has been proved for a certain  . We shall prove the theorem for
. We shall prove the theorem for  convex sets. Suppose we are given
convex sets. Suppose we are given  convex sets
convex sets  in the plane such that any 3 of them contain a common point. For each label
in the plane such that any 3 of them contain a common point. For each label 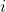 from
from 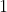 to
to  , pick a point
, pick a point 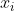 such that it belongs to all the
such that it belongs to all the  convex sets except possibly
convex sets except possibly  . This is possible by our induction hypothesis. Now consider
. This is possible by our induction hypothesis. Now consider  . By our lemma, relabeling our indices if necessary, we can assume that there exists a label
. By our lemma, relabeling our indices if necessary, we can assume that there exists a label 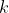 ,
,  , such that the convex hulls of
, such that the convex hulls of  and
and  contain a common point. Let's call this common point
contain a common point. Let's call this common point 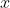 . Since
. Since 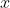 belongs to the convex hull of
belongs to the convex hull of  , it belongs to
, it belongs to  for all
for all  ; here we make use of the assumptions that the sets
; here we make use of the assumptions that the sets  are convex. Similarly, since
are convex. Similarly, since 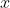 belongs to the convex hull of
belongs to the convex hull of  , it belongs to
, it belongs to  for all
for all  . Hence
. Hence 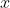 is contained in all the
is contained in all the  sets
sets  , and this completes the proof.
, and this completes the proof.
The theorem actually holds in for any
for any 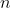 . One just needs to replace 3 by
. One just needs to replace 3 by 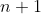 in the statement of the theorem. The proof and the lemma works equally well in high dimensions; one just needs to replace every 4 by
in the statement of the theorem. The proof and the lemma works equally well in high dimensions; one just needs to replace every 4 by  there.
there.
One interesting question came out of my discussion with my friend though. Suppose now we are in a finite dimensional vector space over a finite field (instead of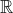 ). It of course doesn't make sense to talk about convexity there. However, we may replace "convex sets" by "affine linear subspaces" (translates of vector subspaces) and ask the following question:
). It of course doesn't make sense to talk about convexity there. However, we may replace "convex sets" by "affine linear subspaces" (translates of vector subspaces) and ask the following question:
Let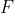 be a finite field. Suppose we are given a finite number of affine linear subspaces of
be a finite field. Suppose we are given a finite number of affine linear subspaces of  where any
where any 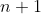 of them intersect. Must the intersection of all the given affine linear subspaces be non-empty?
of them intersect. Must the intersection of all the given affine linear subspaces be non-empty?
I am not sure how interesting or difficult this problem is; perhaps there is a really easy solution to this problem, and we haven't put much effort into thinking about it anyway. But if some of you come up with any idea on how to approach or solve the problem, I'd be interested to know.
If we are given a finite number of convex sets in the plane and any 3 of them contain a common point, then there is a point that is common to all these convex sets.
You may wish to draw a picture to convince yourself of this theorem before proceeding.
The proof is based on the following lemma:
Letbe any collection of 4 points in the plane. Then we can partition this collection into a disjoint union
such that the convex hull of
intersects the convex hull of
.
(If some of you are not familiar with the notions used in the above statement, here is another (more clumsy) way of saying the same thing: Let
The proof of the lemma is based on the following linear algebra argument:
Consider the system of 3 linear equations in 4 unknown real numbers
(The second equation is a vector equation in the plane, so it actually represents two linear equations.)
A well-known linear algebra fact is that if you have 3 linear equations in 4 unknowns, you can always find a non-zero solution to the equation. Suppose by abuse of notation
Now from the first defining equation of
Since we assumed
From the second defining equation of
Dividing both sides of the equation by
But the left hand side of this equation is a convex linear combination of the points
Next, we shall prove the theorem by induction on the number
The theorem actually holds in
One interesting question came out of my discussion with my friend though. Suppose now we are in a finite dimensional vector space over a finite field (instead of
Let
I am not sure how interesting or difficult this problem is; perhaps there is a really easy solution to this problem, and we haven't put much effort into thinking about it anyway. But if some of you come up with any idea on how to approach or solve the problem, I'd be interested to know.
訂閱:
文章 (Atom)