0.999... = 1?

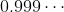
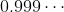
　　很多人應該在不少科普叢書或網上討論區見過「 = 1？」這問題。我們只需簡單的極限概念（甚至幾何級數和的概念），便知道這答案是肯定的， 等於 1。可是每當有人在討論區提出這問題時，答案總是似是而非，甚至出現很多不同的悖證。我不打算在這裏再證明一次這道命題，但卻想簡單闡釋以前見過的常見謬誤。

謬誤一：

　　 和 1 這兩個數的寫法不相同，它們怎可能一樣？

解釋：

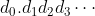
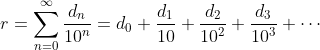
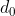
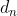
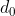
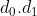
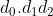
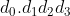
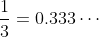
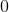
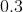
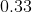
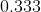
　　我們先說明甚麼是小數。如果我們以小數形式寫成某實數 r 時，其表達式為 ，我們表示 ，其中 是整數部分，而 是第 n 個小數位。這是一個無窮項的和，因此我們求這個和時其實正在求某數列的極限。這個數列是 、、、、……。例如，我們指 時，其實指 是 、、、、……這數列的極限。

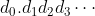
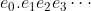
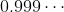
　　在這個定義裏，我們沒特別指明表示法是唯一的。換句話說，我們沒指出實數 r 不可以擁有兩種表達式 和 。這就好像兩個分數式 和 的值相同一樣。既然如此，為甚麼 不可以和 1 相同？

謬誤二：

　　我們不會將小數寫成以無窮個 9 結尾，因此 這寫法根本不成立。

解釋：

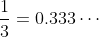
　　如果你接受 可以以無窮個 3 結尾，為甚麼無窮個 9 不可以？平日人們不會將 1 寫成 ，並不代表不可以這樣寫。　

謬誤三：

　　 的整數部分明明是 0，而 1 的整數部分是 1，為何它們會相同？

解釋：

　　請參看謬誤一。同一個實數可以擁有超過一種表示法。

謬誤四：

　　 只是非常接近 1，但不相同。

解釋：

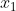
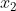
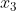
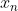
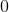
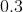
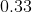
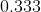
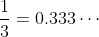
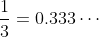
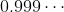
　　請參看謬誤一。無窮小數的表達式是數列的極限。籠統地說，若一個數列 、、、……的極限是 L，則我們指當 n 愈來愈大時， 愈來愈接近 L。（當然這說法有點瑕疪，但極限的定義本來就依賴這想法而來。我們不在此深究這句子和極限的定義的分別。）以 為例，因為 、、、……這數列漸漸趨近 ，所以我們說 。我們指的是數列的極限是 ，而並非數列當中任何一項是 。如果你接受 ，為何不接受 = 1？