日期：2009 年 11 月 20 日（星期五）
時間：下午 6 時 30 分至 8 時 30 分
地點：香港城市大學教學樓四樓 LT18 演講廳
講者：曾淵滄博士
講題：投資全攻略
簡介：
本講座旨在從科學角度與重點介紹甚麼是管理科學，亦討論管理科學如何在投資及財務應用方面所扮演之角色。本講座亦專為有志參加快張開辦的統計學課程而設。
有關其他詳情及報名方法，可瀏覽這裡。
（如果無法載入，可複製網址 http://hkage.org.hk/b5/new/Students/ma/0910003/poster.pdf）
2009年10月19日 星期一
死後的paper？
前兩天聽了一個關於random graph的seminar，回到辦公室就拿起Janson, Luczak和Rucinski的Random Graphs查一些terms的意思。隨手一揭，見到Erdős, Suen和Winkler在1995年一起出了一份paper。當時我想如果這是Paul Erdős的話，他不是已經離世很久了嗎？但查一查wiki，才知道他是在1996年離世的。
但另外查一查DBLP，竟發現Paul Erdős直到2006年為止仍然有聯名的paper發。究竟是因為其他的作者在十多年前和他討論得出成果，所以將Paul Erdős的名字寫在作者欄上，還是這個世界上有另一個Paul Erdos呢？煩請有識之士指點迷津。
但另外查一查DBLP，竟發現Paul Erdős直到2006年為止仍然有聯名的paper發。究竟是因為其他的作者在十多年前和他討論得出成果，所以將Paul Erdős的名字寫在作者欄上，還是這個世界上有另一個Paul Erdos呢？煩請有識之士指點迷津。
2009年10月14日 星期三
AM-GM 不等式的幾個證明（六）
看見 Kahoo 給了 AM-GM 不等式這麼多個精彩的證明，不禁想再來一個用微分和凸函数 (convex functions) 的。
這裏我們只需留意對任意實數 x 和 a，
這不等式可以用很多不同的方法來證明，其中要想清楚當中的概念的，比較好的方法，是留意
是一凸函數，故其導數是遞增的，用中值定理即可推出上述不等式。（也可以不失一般性假設
，從而用一元微積分或 的 Taylor 展開求得此不等式。）
有了這不等式以後，對正數
，
這裏 a 可以是任何實數。把上列的不等式平均起來，得到
------(1)
取
，則
從而 AM-GM 不等式得證。事實上不等式 (1) 的右邊是一關於 a 的函數，左邊則跟 a 無關，所以我們會取的 a 使得 (1) 的右邊達至最大值，而這正是我們上面這樣取 a 的原因。
這證明的一個好處，是我們可以用同樣的辦法證明以下這個 AM-GM 不等式的推廣：對任意
，和任意正數 
使得 
，有
從上面的討論可知，其實 AM-GM 不等式是函數 的 convexity 的反映。對任何的凸函數 f，我們都有 Jensen 不等式，詳見 wikipedia。
這裏我們只需留意對任意實數 x 和 a，
這不等式可以用很多不同的方法來證明，其中要想清楚當中的概念的，比較好的方法，是留意
是一凸函數，故其導數是遞增的，用中值定理即可推出上述不等式。（也可以不失一般性假設，從而用一元微積分或 的 Taylor 展開求得此不等式。）有了這不等式以後，對正數
，這裏 a 可以是任何實數。把上列的不等式平均起來，得到
------(1)取
，則從而 AM-GM 不等式得證。事實上不等式 (1) 的右邊是一關於 a 的函數，左邊則跟 a 無關，所以我們會取的 a 使得 (1) 的右邊達至最大值，而這正是我們上面這樣取 a 的原因。
這證明的一個好處，是我們可以用同樣的辦法證明以下這個 AM-GM 不等式的推廣：對任意
，和任意正數 使得 ，有從上面的討論可知，其實 AM-GM 不等式是函數
的 convexity 的反映。對任何的凸函數 f，我們都有 Jensen 不等式，詳見 wikipedia。
2009年10月11日 星期日
AM-GM 不等式的幾個證明（五）
作為本系列的完結篇，我們看看 AM-GM 不等式的一個不用數學歸納法的證明。本證明主要用到排序不等式，此不等式指出若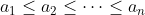 
而 
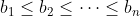，那麼當我們把這些 ai 和 bi「配對相乘再相加」時，有以下不等式：
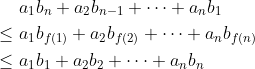
這裡 f(1)、f(2)、…、f(n) 是 1, 2, ..., n 的一個任意排列，而以上不等式中的三行分別叫「逆序和」、「亂序和」和「順序和」。不等式看起來有點複雜，但其實背後意念很簡單：假設一批學生分 n 組比賽（人數分別是 a1、a2、…、an），而每組均選擇 n 種隊服中的一種（價錢分別是 b1、b2、…、bn），那麼最省錢的自然是越多人的組別使用越便宜的隊服（即逆序和），最花錢的自然是越多人的組別使用越貴的隊服（即順序和）。利用排序不等式，不難證明對任意正數 y1、y2、…、yn 皆有
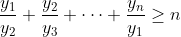
（不失一般性設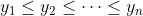
，並設 
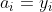和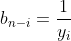 
，再使用「亂序和 ≧ 逆序和」即可）。
現在我們用以上結果來證明 AM-GM 不等式。不妨設 x1x2…xn = 1（這可通過代換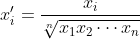
得到），並設
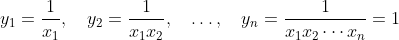即可得
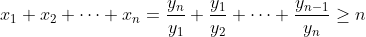
從而證明了 AM-GM 不等式。
順帶一提，排序不等式的等號成立當且僅當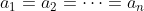
或 
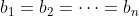，大家不妨試試由此導出 AM-GM 不等式的等號成立當且僅當 
。
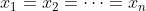而 ，那麼當我們把這些 ai 和 bi「配對相乘再相加」時，有以下不等式：這裡 f(1)、f(2)、…、f(n) 是 1, 2, ..., n 的一個任意排列，而以上不等式中的三行分別叫「逆序和」、「亂序和」和「順序和」。不等式看起來有點複雜，但其實背後意念很簡單：假設一批學生分 n 組比賽（人數分別是 a1、a2、…、an），而每組均選擇 n 種隊服中的一種（價錢分別是 b1、b2、…、bn），那麼最省錢的自然是越多人的組別使用越便宜的隊服（即逆序和），最花錢的自然是越多人的組別使用越貴的隊服（即順序和）。利用排序不等式，不難證明對任意正數 y1、y2、…、yn 皆有
（不失一般性設
，並設 和 ，再使用「亂序和 ≧ 逆序和」即可）。現在我們用以上結果來證明 AM-GM 不等式。不妨設 x1x2…xn = 1（這可通過代換
得到），並設順帶一提，排序不等式的等號成立當且僅當
或 ，大家不妨試試由此導出 AM-GM 不等式的等號成立當且僅當 。
2009年10月6日 星期二
Gil Kalai's Seminar
上週四Hebrew University of Jerusalem和Yale University教授Gil Kalai來了Courant Institute講seminar。大家可能對這個名字有點印象，因為我曾在一篇手記 "Test Your Intuition"中提及他的網誌"Combinatorics and More"。
平時同一時段的"theory seminar"，有多於15人已屬罕見，但今次Prof. Kalai來講seminar卻吸引了38人來。平時有空位剩的房間一下子全院滿座，還有幾個人坐地下聽。
Prof. Kalai講了三個猜想，其中一個比較易懂和有趣，可以在這裏講講。
設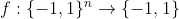
。我們可以進行一個"Fourier Transform"，即寫成
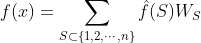，當中
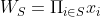（這與一般Fourier Series中的
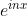的角色相同。）假設
，若每一個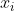
均獨立地有機會率 t 改變值（即由-1變成1或由1變成-1），若
的機會很高，我們就可說 f 是noise stable。
甚麼情況下 f 是noise stable呢？Prof. Kalai舉了一個有趣的例子，就是說美國總統選舉，若Obama得票的數目是單數他就當選，否則McCain當選，這個選舉就很"noisy"，對吧？由此例子見到，noise stable的函數，它的Fourier expansion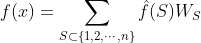中，當S是一個較大的集合時，
的值就應該很小。
平時同一時段的"theory seminar"，有多於15人已屬罕見，但今次Prof. Kalai來講seminar卻吸引了38人來。平時有空位剩的房間一下子全院滿座，還有幾個人坐地下聽。
Prof. Kalai講了三個猜想，其中一個比較易懂和有趣，可以在這裏講講。
設
。我們可以進行一個"Fourier Transform"，即寫成，當中（這與一般Fourier Series中的的角色相同。）假設，若每一個均獨立地有機會率 t 改變值（即由-1變成1或由1變成-1），若的機會很高，我們就可說 f 是noise stable。甚麼情況下 f 是noise stable呢？Prof. Kalai舉了一個有趣的例子，就是說美國總統選舉，若Obama得票的數目是單數他就當選，否則McCain當選，這個選舉就很"noisy"，對吧？由此例子見到，noise stable的函數，它的Fourier expansion
中，當S是一個較大的集合時，的值就應該很小。
2009年10月5日 星期一
2009年10月1日 星期四
AM-GM 不等式的幾個證明（四）
上回看過 AM-GM 不等式的一個「普通數學歸納法」證明。這裡我們再看三個類似的證明。一如之前，設 xi 為正數，並已知 AM-GM 不等式對 n=1 和 n=2 成立。
假設 n=k 時 AM-GM 不等式成立，並考慮 n=k+1 時的情況。如果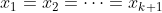
，則 AM-GM 不等式顯然成立，否則不妨設各數中 x1 最小，xk+1 最大，那麼這 k+1 個數的平均（不論是算術平均或是幾何平均）均大於 x1 而小於 xk+1。以下用三個方法證明 n=k+1 的情況。
方法一
設
。由歸納假設可知
，
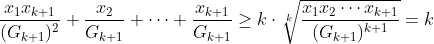從而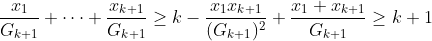
，其中最後一個不等式成立是因為
。
方法二
設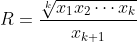
，則 
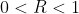，故此
方法三
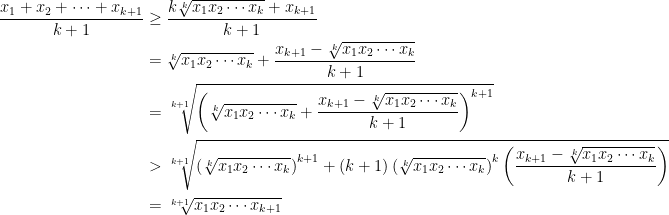
除了用數學歸納法外，AM-GM 不等式還可以用其他方法來證明，我們下回再看。
假設 n=k 時 AM-GM 不等式成立，並考慮 n=k+1 時的情況。如果
，則 AM-GM 不等式顯然成立，否則不妨設各數中 x1 最小，xk+1 最大，那麼這 k+1 個數的平均（不論是算術平均或是幾何平均）均大於 x1 而小於 xk+1。以下用三個方法證明 n=k+1 的情況。方法一
設
。由歸納假設可知，從而
，其中最後一個不等式成立是因為。方法二
設
，則 ，故此除了用數學歸納法外，AM-GM 不等式還可以用其他方法來證明，我們下回再看。
訂閱：
文章 (Atom)