一幅啤牌52隻,發展出很多趣的遊戲出來,包括橋牌、「鋤大D」、廿一點等等。每盤遊戲結束,指定動作就是洗牌。相信你一定見到有人隨便「cut兩cut」就算,但亦有人洗一次牌洗成分鐘,有點掃興的味道。
究竟,洗牌要洗幾多次先「夠」?要回答這條問題前,首先要定義甚麼是「夠」。從概率學上,「夠」可以定義為每一個可能性出現的機會都(大約)相等。1992年Bayer和Diaconis研究了以下一種洗牌方法(以下一段不只針對啤牌;一幅牌可以有
n隻):
首先一幅牌排成一疊,然後每隻牌順序抽出,再擲骰仔決定放左面還是右面:若是單數放左面,若是雙數放右面。然後將左面的牌疊在右面的牌的上方。
這種洗牌方法叫inverse Gilbert-Shannon-Reeds shuffle (inverse GSR shuffle)。Bayer和Diaconis証明了若進行大約
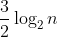
次inverse GSR shuffle,副牌就大約「洗勻」了。換言之,對啤牌來說,需要洗牌大約 8.55 次。
當然,現實中用inverse GSR shuffle未免太慢了(擲52次骰仔,每次1秒,再加其餘動作,最少也要1分鐘吧)。但大家想想,若inverse GSR shuffle如兩段前所述,那麼
non-inverse GSR shuffle會是怎樣的?大家又是否覺得似曾相識呢?
-----
Below is for more advanced math students. Only people who have some background on Markov Chain theory should continue reading:
For those who know about Markov Chain theory, you may easily see that it is a Markov process. As every element in the symmetric group has an inverse, it is easy to observe that the eigenvector with eigenvalue 1 is indeed the "uniform distribution vector".
The period of the corresponding stochastic matrix must be 1, since there is non-zero probability that the inverse GSR shuffle remains the deck unchanged. Hence by Perron-Frobenius theorem, all other eigenvectors must be with eigenvalue of modulus strictly less than 1. So after shuffling sufficiently many times, no matter how the intial distribution is, it must converge to the unifrom distribution.
In other words, you may say converging to uniform distribution is an immediate result of Perron-Frobenius theorem. Bayer and Diaconis were analyzing
how fast the convergence is.
時也成立,從而有