有些名言充滿數學哲理，本文選談兩個和概率論有關的名言。
上得山多終遇虎
這句話原指走到山上要面對老虎帶來的危險，即使一次沒有遇到，但如果不斷上山的話，總會有遇到老虎的一天，通常用作比喻做壞事的人終會受到制裁。這話背後有甚麼數學哲理呢？假設每次上山「遇虎」的概率為 p (>0)，且上山 n 次後遇虎最少一次的概率是 Pn，則 Pn = 1 - (1-p)n，故此不難發現當 n 趨向無限大時，Pn 的值趨向 1，應驗了「終遇虎」的結論！
一鳥在手勝過二鳥在林
這句話相信是出自英語的「One bird in hand is worth two in the bush」，不論中英文版本都有一些「變種」，主要是把「二」變成其他數字，不過意思也都相同，就是說「實在」勝過「浮雲」，有時則用以比喻要珍惜現在，別奢求無法得到的東西。
這話背後又有甚麼數學哲理？一鳥在手是否勝過二鳥在林，表面上視乎「在林」的鳥可以「到手」的概率 p，也就是視乎「二鳥在林」的期望值（expected value）。如果 p>0.5 的話，則「二鳥在林」的期望值是比「一鳥」高的。那麼為甚麼有一鳥在手「勝過」二鳥在林的說法呢？
很多時候，我們下決定時都不只看期望值。舉例說，假設你的身家有 n 元，現讓你從一副紙牌中抽兩張，如果抽到黑桃 A 和紅心 A 的話獎你 100000 n 元，否則輸掉 n 元，遊戲只可玩一次。這個遊戲的期望值是個很大的正數（當然是相對 n 而言），你願意參加嗎？ 除了期望值外，離差（dispersion）也會影響我們的決定，例如標準差（standard variation）是一個常見的離差指標。一般來說，我們希望離差越小越好，於是以上遊戲中正數的期望值便不足以彌補很大的離差。
這就解釋了一鳥在手為何可以勝過二鳥在林了 -- 因為「一鳥在手」時標準差是零，而「二鳥在林」時標準差是正數呢！
2009年6月22日 星期一
2009年6月20日 星期六
Convolution Technique in Generating Function (2)
It is quite unexpected that the second part of this passage is posted three months later. Anyway, let me post the link to the first part of this passage. Here, I am going to discuss another counting problem which we can use convolution technique to solve.
Let me recall the key idea again. Convolution of generating functions can be useful when we try to count a class of combinatorial objects, while these objects can be constructed by joining two smaller objects of size k and M-k.
Here comes the question, which looks really unfavourite when you first see it. An n by n square matrix M satisfies the following conditions: (1) every entry is a non-negative integer; (2) the sum of entries in each column is n-1; (3) for any two entries which are both positive, denote the coordinates by
and 
, then 
.
Below shows a few 4 by 4 matrices which satisfy the three conditions:
, 
, 
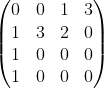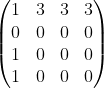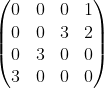
The first two conditions can be easily visualized. The third condition can be visualized as follows: for any non-zero entry, its north-west and south-east direction entries must be all zero.
I will generalize by counting the number of p (number of columns) by q (number of rows) matrices satisfying the three conditions (note: the sum of each column is fixed to be n-1). Let the number of such p by q matrices be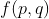
. Then our target is finding 
.
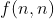Suppose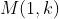
denote the entry in the first column such that it is the toppest entry in the first column with non-zero entries (i.e. 
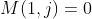for all 
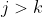.) So the matrix looks like:
The black parts will be with all zero entries (by definition of 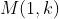and by condition 3). So the construction of this matrix can be divided into two parts:
a) constructing a 1 by k sub-matrix such that
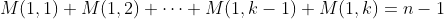with 
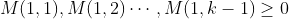and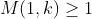 
.
b) constructing the (p-1) by (q-k+1) sub-matrix A such that the three conditions are satisfied.
By simple combinatorics, there are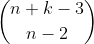
ways to construct part a) (if you do not see why, read the notes "Combinations and Permutations" in Mathematical Database; in particular, it is page 10 to 14) and by definition, there are 
ways to construct part b). As k can be any value between 1 and q (inclusive), we have the recurrence relation:
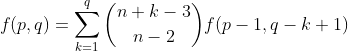
Compare this recurrence to the one for Catalan numbers. Do you see the similarity? If so, try to continue. I will complete this passage a few days later (hopefully...).
Let me recall the key idea again. Convolution of generating functions can be useful when we try to count a class of combinatorial objects, while these objects can be constructed by joining two smaller objects of size k and M-k.
Here comes the question, which looks really unfavourite when you first see it. An n by n square matrix M satisfies the following conditions: (1) every entry is a non-negative integer; (2) the sum of entries in each column is n-1; (3) for any two entries which are both positive, denote the coordinates by
Below shows a few 4 by 4 matrices which satisfy the three conditions:
The first two conditions can be easily visualized. The third condition can be visualized as follows: for any non-zero entry, its north-west and south-east direction entries must be all zero.
I will generalize by counting the number of p (number of columns) by q (number of rows) matrices satisfying the three conditions (note: the sum of each column is fixed to be n-1). Let the number of such p by q matrices be
Suppose
The black parts will be with all zero entries (by definition of a) constructing a 1 by k sub-matrix such that
b) constructing the (p-1) by (q-k+1) sub-matrix A such that the three conditions are satisfied.
By simple combinatorics, there are
Compare this recurrence to the one for Catalan numbers. Do you see the similarity? If so, try to continue. I will complete this passage a few days later (hopefully...).
2009年6月10日 星期三
概率證明
有些時候，我們可以利用概率的性質來證明一些組合題。即使題目本身看來和概率毫不相干，但加入了概率的考慮往往可以讓我們得出一個簡潔的證明。以下提供一個例子。
問題：
某學校響應微調政策，開辦的 n 個科目均設中文班和英文班。每位同學均可自由選讀不同的科目，數量不限，但同一科目不可同時報讀中文班和英文班。已知對任意兩個科目，均存在一名學生以不同語文同時修讀兩科。若每科最多有 10 名學生修讀，求 n 的最大可能值。
大家看下去前，不妨先停下來自己動動腦筋。
解答：
n 的最大可能值是 1024。
我們首先注意到 n=1024 是可能的：如果全校有 10 位學生，每人均報讀全部 1024 個科目，且學生 i 報讀第 j 個科目的中文班當且僅當 j 的二進制表示中右方數起的第 i 個位是 1（否則報讀第 j 個科目的英文班），則不難檢查得知這符合題中的條件。
以下證明 n 不可大於 1024。假設學生入學時會被隨機編成「中文人」或「英文人」。設 Ei 表示事件「第 i 個科目的學生全部選讀了對應自己身份的語文班」，則由於每科最多有 10 名學生修讀，故 P(Ei) ≧ 1/210 = 1/1024。再者，由「對任意兩個科目，均存在一名學生以不同語文同時修讀兩科」可知 E1、E2、…、En 是互斥事件，故此
從而必有 n≦1024。
這個帶點神秘感的概率題解，某程度上其實對應一些數算的技巧，再用概率加以包裝。概率證明還可以處理一些更複雜的情況，例如可以使用 Lovasz local lemma 來處理一些難以準確計算的概率，有興趣的讀者可點擊上方的連結細看。順帶一提，證明以上定理的 Lovasz 曾在國際數學奧林匹克（IMO）奪得三金一銀，而他的兒子至今亦已在 IMO 奪得一金一銀！
問題：
某學校響應微調政策，開辦的 n 個科目均設中文班和英文班。每位同學均可自由選讀不同的科目，數量不限，但同一科目不可同時報讀中文班和英文班。已知對任意兩個科目，均存在一名學生以不同語文同時修讀兩科。若每科最多有 10 名學生修讀，求 n 的最大可能值。
大家看下去前，不妨先停下來自己動動腦筋。
解答：
n 的最大可能值是 1024。
我們首先注意到 n=1024 是可能的：如果全校有 10 位學生，每人均報讀全部 1024 個科目，且學生 i 報讀第 j 個科目的中文班當且僅當 j 的二進制表示中右方數起的第 i 個位是 1（否則報讀第 j 個科目的英文班），則不難檢查得知這符合題中的條件。
以下證明 n 不可大於 1024。假設學生入學時會被隨機編成「中文人」或「英文人」。設 Ei 表示事件「第 i 個科目的學生全部選讀了對應自己身份的語文班」，則由於每科最多有 10 名學生修讀，故 P(Ei) ≧ 1/210 = 1/1024。再者，由「對任意兩個科目，均存在一名學生以不同語文同時修讀兩科」可知 E1、E2、…、En 是互斥事件，故此
1 ≧ P(E1∪E2∪…∪En) = P(E1) + P(E2) + ... + P(En) ≧ n/1024，
從而必有 n≦1024。
這個帶點神秘感的概率題解，某程度上其實對應一些數算的技巧，再用概率加以包裝。概率證明還可以處理一些更複雜的情況，例如可以使用 Lovasz local lemma 來處理一些難以準確計算的概率，有興趣的讀者可點擊上方的連結細看。順帶一提，證明以上定理的 Lovasz 曾在國際數學奧林匹克（IMO）奪得三金一銀，而他的兒子至今亦已在 IMO 奪得一金一銀！
訂閱：
文章 (Atom)