數學資料庫手記: Convolution Technique in Generating Function (1)

When I was the TA of the course "Combinatorial Analysis" in HKUST, I told students that one of the powerful properties of generating function is "convolution".

(*)To combinatorially construct an object of size n, it is a common way to first construct two smaller objects of size k and M-k (where M is a function of n, say, n or (n-1)), and then join the two smaller objects together.

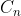
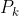
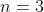
The most famous example must be finding the Catalan Number. Catalan Number $C_n$ is counting the number of ways to write n "+1" and n "-1" in a row such that the for $1\leq k\leq 2n$ , the sum of the first k terms (we denote it by $P_k$ ) is NOT negative. For example, when $n=3$ , "+1 +1 -1 -1 +1 -1" and "+1 +1 +1 -1 -1 -1" satisfy the requirement while "+1 +1 -1 -1 -1 +1" does not (the first five terms sum to -1, which is negative).

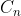
Now we find out a recurrence of $C_n$ using the technique mentioned in (*). We denote the i^th term be $x_i$ .

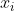
You know, $x_1=1$ and $P_{2n}=0$ . So there exists a smallest $k\geq 0$ such that $P_{2(k+1)}=0$ . ( $P_a=0$ is impossible if a is odd.)

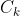
The terms between $x_2$ and $x_{2k}$ (inclusive) must itself form a Catalan sequence of size 2k. The reason is, if it is not a Catalan sequence, then $x_2+x_3+\cdots+x_{2a}=-1$ for some $1\leq a\leq k$ , and then , $P_{2a}=0$ , i.e. contradicting to the assumption that k is the smallest integer such that $P_{2k}=0$ . Hence, there are $C_k$ ways to fill in $x_2$ to $x_{2k}$ .

Similarly, the terms between $x_{2k+3}$ and $x_{2n}$ (inclusive) must itself form a Catalan sequence of size 2n-2k-2. Hence, there are $C_{n-1-k}$ ways to fill in $x_{2k+3}$ to $x_{2n}$ .

Hence, if k is the smallest integer such that $P_{2k}=0$ , there are $C_k C_{n-1-k}$ ways to construct a Catalan sequence of size 2n. The value of k can be varied from 0 to n-1. So we have the "convolution recurrence":

$C_n = \sum_{k=0}^{n-1} C_k C_{n-1-k}$

Now define the generating function $C(z) = C_0 + C_1 z + C_2 z^2 + C_3 z^3 + \cdots$ . Reader can check that (by comparing coefficients)

$C(z) = z C(z)^2 + 1$

This is what we called "convolution" in the first paragraph. When someone multiplies two polynomials, to find the coefficient of $z^i$ , he has to multiply the term $x_j$ in the first polynomial to the term $x_{i-j}$ in the second polynomial. This "one increase, one decrease" property for polynomial multiplication gives the great convenience for the generating function to handle the convolution recurrence for Catalan numbers.

Now, the remaining task is purely algebraic. For $C(z) = z C(z)^2 + 1$ , treat $C(z)$ as a variable, then it becomes a quadratic equation. By quadratic formula, we have

$C(z) = \frac{1\pm\sqrt{1-4z}}{2z}$

Requiring $C(z)$ has no pole at $z=0$ , we reject $C(z)=\frac{1+\sqrt{1-4z}}{2z}$ and hence

$C(z)=\frac{1-\sqrt{1-4z}}{2z}$
Lastly, apply Newton's binomial theorem to $\sqrt{1-4z}$ , we arrive at the fact that

$C_n = [z^n] C(z) = -\frac{[z^{n+1}]\sqrt{1-4z}}{2} = -\frac{1}{2}\binom{\frac{1}{2}}{n+1} (-4)^{n+1}= -\frac{1}{2}\frac{\frac{1}{2}\times\frac{-1}{2}\times\frac{-3}{2}\times\cdots\times\frac{-(2n-1)}{2}}{(n+1)!}(-4)^{n+1}=(-1)^{2n+2}4^{n+1}\left(\frac{1}{2}\right)^{n+2}\frac{(1)(3)(5)\cdots(2n-1)}{(n+1)!}=2^n\frac{(2n)!}{2^n n! (n+1)!}=\frac{1}{n+1}\binom{2n}{n}$

數學資料庫手記

2009年3月9日星期一

Convolution Technique in Generating Function (1)

沒有留言:

著作人

stat

網誌存檔