1) Suppose
2) S contains all elements
2009年12月11日 星期五
Two Analysis Problems
Recently I heard two problems in analysis, both I think are interesting, and they do not require too deep knowledge in analysis, which is the kind of questions I like most. Share here.
1) Suppose
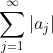
converges. Also, for each positive integer k, it is known that 
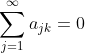
(just to avoid confusion, allow me clarify here that jk means "j times k"). Prove that 
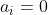
for all positive integers i.
2) S contains all elements
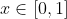
such that for any 
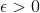
, there exists a rational number 
(where p,q are positive integers) satisfying 
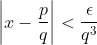
. Prove that S is uncountable.
1) Suppose
2) S contains all elements
訂閱：
張貼留言 (Atom)
3 則留言:
For the first problem, it is even more interesting to ask whether there are non-zero examples when the assumption on absolute convergence is removed. Can someone give such an example?
For the second one, it follows from Baire Category Theorem, right?
To Singmay: just seen your comment, thinking...
To Polam: I did not realize that Baire Category Theorem is useful here. I just use elementary approach to show that S contains a subset which is equivalent to 2^N, which is uncountable.
張貼留言