[轉貼]A Sad Story in Academia

This is a sad story in academia.

I post here not to blame any particular person, but wanna to let ordinary readers, which may not be in academia, sees another view of the academia, which may have been phenotyped by media.

I decided to pursue PhD study in America, one main reason due to my interest in the subject of Math and CS, and another reason is although there can be such sad stories in academia, as far as I know, in most cases, the truth is still ultimately respected in academia.

MAC2010 決賽作品感想

有不少文章類的作品臨時採用 html 格式 ..
這是極不明智的。

普遍作品也有以下人為錯誤.

(1) 「C Drive 大法」 (有的作品甚至乎連用戶名稱也放在連結上..)
(2) 全形’ 和 半形'
(3) Flash 亂碼問題 (UTF-8 , BIG-5 與 Locale 的設定)
(4) 放錯 link (如 main.html 及 X theory main.html 的分別"
(5) htm 與 html 檔名不分

嚴重的甚至連檔案也不能開啟...
以致變成空白檔

(如把上述因素計算在內....
決賽名單中至少有兩份作品可當成 "not submitted")

以小說作為題材的純文字文章，可參考 一些輕小說網站的做法也可以.

圖文並茂的...建議用 pdf 格式儲存
以確保 評判在任何電腦上開啟閱讀時仍保持 原有的排版等.
(html 絕不能確保排版, 完全取決於評判的電腦)

直角三角形的中線（四）

之前已經看過這個幾何問題的七個解。這裡我們再多看三個。如果大家有其他解法的話，歡迎隨時提供。

解法八

設 AD = DC = x，∠BAC = y，則 AB = 2x cos y。在 △ABD 中運用餘弦定律（cosine law），我們有

BD² = (2x cos y)² + x² - 2 (2x cos y) (x) cos y = x²

從而 DA = DB = DC = x。

解法九

設 ∠ADB = y，則 ∠CDB = 180^o - y。分別對 △ABD 和 △CBD 運用餘弦定律，我們有

　　　AB² = DA² + DB² - 2 (DA) (DB) cos y
　　　BC² = DC² + DB² - 2 (DC) (DB) cos (180^o - y)

由於 DA = DC，AB² + BC² = AC² = 4 DA²，且 cos y = -cos (180^o - y)，故加起以上兩式可得

　　　4 DA² = 2 DA² + 2 DB²

從而 DB = DA (= DC)。

解法十

由於 BA 與 BC 垂直，且 D 是 AC 的中點，故此

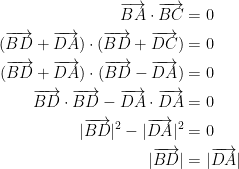
即 DB = DA (= DC)。

直角三角形的中線（三）

繼續這個幾何問題的其他解法。

解法五

考慮 △ABC 的外接圓：

由於 ∠ABC = 90^o，所以 AC 是圓的直徑，D 是圓的圓心。由於 DA、DB、DC 都是圓的半徑，故此它們的長度相等。

解法六

沿 AB 反射 C 到 C'，我們有 BC = BC'。由中點定理可知 AC' // DB。設 E 為 C 到 AC’ 的垂足，則 A、E、B、C 四點共圓，故 ∠BEC = ∠BAC。


設 CE 與 BD 的交點為 F，則 ∠DFC = 90^o，故由截線定理可知 EF = FC。因此 △BEF 和 △BCF 全等 (SAS)，從而 ∠BCE = ∠BEC = ∠BAC。

由此可知 ∠ABD = 90^o - ∠FBC = ∠BCE = ∠BAC，故 DB = DA (= DC)。

解法七

設 B 為原點，A = (0, 2a)，C = (2c,0)。由於 D 是 AC 的中點，故此 D = (c, a)。經直接計算可知

直角三角形的中線（二）

上回提到一個幾何問題和它的一個解。你想到多少個其他解法呢？這裡我們先看看其中三個：

解法二

設 E 為 AB 的中點。由中點定理可知 ED 與 BC 平行，故 ∠AED = 90^o，從而 △ADE 和 △BDE 全等 (SAS)，因此 DB = DA (= DC)。

解法三

我們知道，三角形中「大角對長邊、小角對短邊」。若 DC = DA > DB，則有 ∠ABD > ∠BAD 和 ∠DBC > ∠DCB，從而 90^o = ∠ABD + ∠DBC > ∠BAD + ∠DCB = 90^o，矛盾。同理，若 DB > DC = DA，則有 ∠ABD < ∠BAD 和 ∠DBC < ∠DCB，從而 90^o = ∠ABD + ∠DBC < ∠BAD + ∠DCB = 90^o，矛盾。

故此 DC = DA = DB 必定成立。

解法四

沿 AB 反射 C 到 C'，我們有 AC = AC' 和 BC = BC'。由中點定理可知 2DB = AC' = AC。由於 D 是 AC 的中點，故此 DB = DA = DC。