Helly's selection theorem

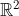
Yesterday a friend of mine showed me a very cute and completely elementary fact about convex sets in the plane, and perhaps I could share it here. It's a classical theorem due to Helly. It actually works in arbitrarily high dimensions, but for clarity of exposition let's restrict ourselves to the Euclidean plane . The theorem is the following:

If we are given a finite number of convex sets in the plane and any 3 of them contain a common point, then there is a point that is common to all these convex sets.

You may wish to draw a picture to convince yourself of this theorem before proceeding.

The proof is based on the following lemma:

Let be any collection of 4 points in the plane. Then we can partition this collection into a disjoint union such that the convex hull of intersects the convex hull of .

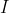
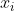
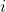
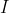
(If some of you are not familiar with the notions used in the above statement, here is another (more clumsy) way of saying the same thing: Let be any 4 points in the plane. Then one can find a set of labels , consisting of some of the numbers 1, 2, 3 and 4, such that the following is true: Let be the collection of points whose label is in , and let be the collection of the remaining points. Let be the smallest convex set containing all the points in , and be the smallest convex set containing all the points in . Then the two sets and contain a common point.)

The proof of the lemma is based on the following linear algebra argument:

Consider the system of 3 linear equations in 4 unknown real numbers :




(The second equation is a vector equation in the plane, so it actually represents two linear equations.)

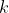
A well-known linear algebra fact is that if you have 3 linear equations in 4 unknowns, you can always find a non-zero solution to the equation. Suppose by abuse of notation is such a solution. By relabelling the points if necessary, we can assume that there is a certain label such that are all positive while are all less than or equal to 0.

Now from the first defining equation of , we have

.

Since we assumed is a non-zero solution, the quantity on the left hand side of the above equation must be positive. Let's call it .

From the second defining equation of , we have

.

Dividing both sides of the equation by , we get

.

But the left hand side of this equation is a convex linear combination of the points , and hence is in the convex hull of ; similarly the right hand side of the equation is in the convex hull of . This completes the proof of the lemma.

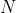
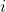
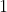
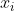
Next, we shall prove the theorem by induction on the number of convex sets involved. The theorem is of course trivial if . Suppose now the theorem has been proved for a certain . We shall prove the theorem for convex sets. Suppose we are given convex sets in the plane such that any 3 of them contain a common point. For each label from to , pick a point such that it belongs to all the convex sets except possibly . This is possible by our induction hypothesis. Now consider . 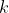By our lemma, relabeling our indices if necessary, we can assume that there exists a label , , such that the convex hulls of and contain a common point. Let's call this common point . 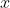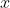Since belongs to the convex hull of , it belongs to for all ; here we make use of the assumptions that the sets are convex. 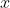Similarly, since belongs to the convex hull of , it belongs to for all . 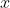Hence is contained in all the sets , and this completes the proof.

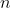
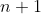
The theorem actually holds in for any . One just needs to replace 3 by in the statement of the theorem. The proof and the lemma works equally well in high dimensions; one just needs to replace every 4 by there.

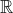
One interesting question came out of my discussion with my friend though. Suppose now we are in a finite dimensional vector space over a finite field (instead of ). It of course doesn't make sense to talk about convexity there. However, we may replace "convex sets" by "affine linear subspaces" (translates of vector subspaces) and ask the following question:

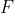
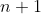
Let be a finite field. Suppose we are given a finite number of affine linear subspaces of where any of them intersect. Must the intersection of all the given affine linear subspaces be non-empty?

I am not sure how interesting or difficult this problem is; perhaps there is a really easy solution to this problem, and we haven't put much effort into thinking about it anyway. But if some of you come up with any idea on how to approach or solve the problem, I'd be interested to know.