電視遊戲和比賽常常講求互動，讓觀眾也參與其中，增加投入感。讓觀眾投票選出比賽得勝者是其中一種常見的互動方法。為了吸引更多觀眾參與，主辦機構會在選中優勝者的參賽者當中，抽出若干幸運兒獲獎。
現假設某比賽只有兩名參賽者，共有 1001 名觀眾投了票選冠軍（票數較多者勝）。主辦機構會抽出一位選中冠軍的觀眾獲得獎品。其中一位觀眾想用概率的知識計算他獲獎的機會。他假設所有人投票都是隨機的，然後這樣想：
「因為所有人都隨機投票，所以兩名參賽者得冠軍的概率相等，皆為 
（注意這裏沒可能平局）。假如我選中冠軍，便可參加抽獎。明顯地，冠軍的得票不少於 501 票（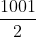
= 500.5），因此我被抽中的機會不多於 
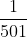。由此可知，我選中冠軍而又被抽中的概率不多於 
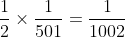。」 整個投票過程裏，每位觀眾的角色都是對稱的。因此這 1001 位觀眾當中任何一位獲獎的機會皆不多於
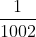
。由此可知，他們當中有人獲獎的機會不多於
。
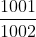
咦，為甚麼這些概率加起來比 1 小？他們當中不是總有一人會得獎嗎？消失了的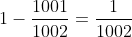 
概率逃到哪裏去？ 現在先讓各位思考和討論，下星期六解題。提示是先考慮小的情況（如 3 人投票），以及將上述各事件寫清楚。還有，問題不在假設了各人隨機投票。
3 則留言:
1)
>概率不多於 1/1002
This is not the exact prob. of each 觀眾 winning the prize, so 1/1002 * 1001 <> 1
2)
其中一位觀眾想用概率的知識計算他獲獎的機會。他假設所有人投票都是隨機的
So, the other 1000 votes are random.
Before he votes, the winning prob. of
參賽者(A, B) should be 1/2.
But his OWN vote is not random for him, so after he voted, the winning prob. of A (say he votes A) is 0.5 + 1/1001 [and Prob(B) = 0.5-1/1001
對，你看出了原因。可是你給出的概率不對。假設他投 A 而其他人投票都隨機投票，A 只需多得 500 票便獲勝。由二項式定理可知，A 勝出的概率為 [C(1000,500) + C(1000,501) + ... + C(1000,1000)]/[2^(1000)]，而非 0.5 + 1/1001。
Right, it is not 0.5!
>其中一位觀眾想用概率的知識計算他獲獎的機會。
>整個投票過程裏，每位觀眾的角色都是對稱的。
It looks the 觀眾(V) knows each voters should have the same prob. (p) in his calculation.
so, by the basic prob. law,
sum of all voters p = 1
p = 1/1001
----
Refer to Andy reply, the 觀眾 V join the game or not, the winning prob. of (A, B) won't change.
(if we accept both A and B are winners if they have equal votes)
張貼留言